Replace fitPlot() with ggplot

Derek H. Ogle

Note

The following packages are loaded for use below. I also set the default ggplot theme to theme_bw() for a classic “black-and-white” plot (rather than the default plot with a gray background).

library(FSA)         ## for peek()
library(emmeans)     ## for emmeans()
library(dplyr)       ## for mutate(), select(), filter(), group_by(), summarize()
library(ggplot2)
theme_set(theme_bw())

Warning

Some functions illustrated below were in the FSA package but have now been removed and put into the non-released FSAmisc package that I maintain. These functions are used below only to show what could be done in older versions of FSA but should now be done as described in this post. DO NOT USE any of the functions below that begin with FSAmisc::.

Introduction

We deprecated fitPlot() from FSA v0.9.0 and fully removed it by the start of 2022. We took this action to make FSA more focused on fisheries applications and to eliminate “black box” functions. fitPlot() was originally designed for students to quickly visualize the results of one- and two-way ANOVAs and simple, indicator variable, and logistic regressions.¹ We now feel that students are better served by learning how to create these visualizations using methods provided by ggplot2, which require more code, but are more modern, flexible, and transparent.

¹ Over time functionality for non-linear regressions was added.

The basic plots produced by fitPlot() are recreated here using ggplot2 to provide a resource to help users that relied on fitPlot() transition to ggplot2.

Example Data

Examples below use the Mirex data set from FSA, which contains the concentration of mirex in the tissue and the body weight of two species of salmon (chinook and coho) captured in six years. The year variable is converted to a factor for modeling purposes and a new variable is created that indicates if the mirex concentration was greater that 0.2 or not. This new variable is used to demonstrate a logistic regression.²

² peek() from FSA is used to examine a portion of the data from evenly-spaced row.

data(Mirex,package="FSA")
Mirex <- Mirex |>
  mutate(year=factor(year),
         gt2=ifelse(mirex>0.2,1,0))
peek(Mirex,n=10)

#R|      year weight mirex species gt2
#R|  1   1977   0.41  0.16 chinook   0
#R|  14  1977   3.29  0.23    coho   1
#R|  27  1982   0.70  0.10    coho   0
#R|  41  1982   5.09  0.27    coho   1
#R|  54  1986   1.82  0.12 chinook   0
#R|  68  1986   8.40  0.13 chinook   0
#R|  81  1992  10.00  0.48 chinook   1
#R|  95  1996   5.70  0.16    coho   0
#R|  108 1999   5.11  0.11    coho   0
#R|  122 1999  11.82  0.09 chinook   0

One-Way ANOVA

The code below fits a one-way ANOVA model to examine if mean weight differs by species.

aov1 <- lm(weight~species,data=Mirex)
anova(aov1)

#R|  Analysis of Variance Table
#R|  
#R|  Response: weight
#R|             Df Sum Sq Mean Sq F value    Pr(>F)    
#R|  species     1  282.4 282.399  27.657 6.404e-07 ***
#R|  Residuals 120 1225.3  10.211                      
#R|  ---
#R|  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

There are at least two simple ways to visualize results from a one-way ANOVA. First, summarized means of raw data with 95% confidence intervals derived from the standard error, sample size, and degrees-of-freedom specific to each group are shown. These are computed below.

sumdata <- Mirex |>
  group_by(species) |>
  summarize(n=n(),
            mn=mean(weight),
            se=se(weight)) |>
  mutate(lci=mn-qt(0.975,df=n-1)*se,
         uci=mn+qt(0.975,df=n-1)*se)
sumdata

#R|  # A tibble: 2 × 6
#R|    species     n    mn    se   lci   uci
#R|    <fct>   <int> <dbl> <dbl> <dbl> <dbl>
#R|  1 chinook    67  6.31 0.474  5.37  7.26
#R|  2 coho       55  3.26 0.279  2.70  3.82

Second, marginal means may be predicted or estimated from the fitted model.³ The main difference from above is that confidence intervals for the marginal means use an “overall” standard deviation and degrees-of-freedom estimated from across all groups. The estimated marginal means may be computed with with emmeans() from emmeans.⁴

³ These are discussed in detail in this vignette from the emmeans package.

⁴ They may also be computed with predict(aov1,newdata=data.frame(species=c("chinook","coho")),interval="confidence").

aov1mc <- emmeans::emmeans(aov1,specs=pairwise~species)
aov1mcs <- summary(aov1mc)
aov1mcs$emmeans

#R|   species emmean    SE  df lower.CL upper.CL
#R|   chinook   6.31 0.390 120     5.54     7.09
#R|   coho      3.26 0.431 120     2.40     4.11
#R|  
#R|  Confidence level used: 0.95

fitPlot() from FSA used the summarized means with 95% confidence intervals for both species.

FSAmisc::fitPlot(aov1)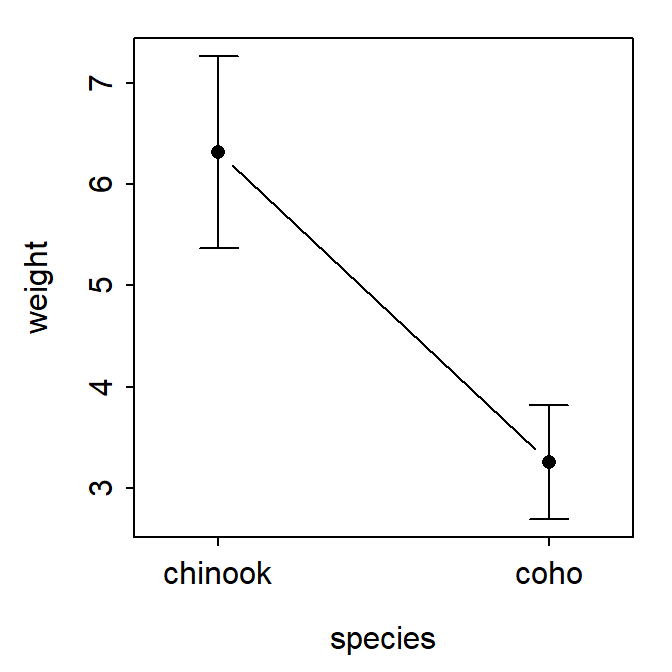

Using Manually Summarized Means

The summarized means saved in sumdata above can be plotted as shown below to recreate the fitPlot() result. width=0.1 in geom_errorbar() is used to reduce the width of the “caps” at the confidence values and group=1 is needed in geom_line() as there is only one point for each factor level. Changes (themes, colors, labels, etc) to this basic plot can be made as usual for ggplot()s (and is illustrated further below).

ggplot(data=sumdata,mapping=aes(x=species)) +
  geom_errorbar(mapping=aes(ymin=lci,ymax=uci),width=0.1) +
  geom_line(mapping=aes(y=mn,group=1)) +
  geom_point(mapping=aes(y=mn))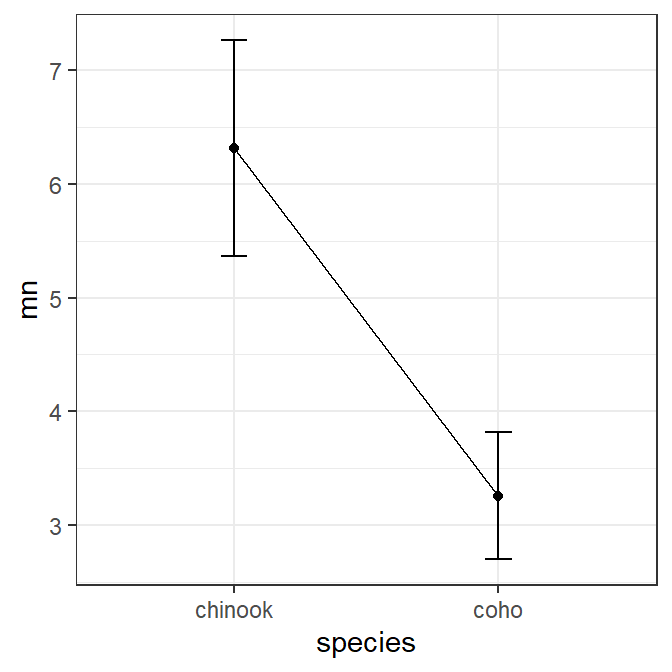

Using Built-In Functions for Summarized Means

This plot can also be constructed without having previously summarized the group means by using stat_summary() coupled with mean_cl_normal() and mean(). Below note how each geom= in each stat_summary() mirrors what was used above. Also note the use of width=0.1 and group=1 here as done above.

ggplot(data=Mirex,mapping=aes(x=species,y=weight)) +  
  stat_summary(fun.data=mean_cl_normal,geom="errorbar",width=0.1) +  
  stat_summary(fun=mean,geom="line",mapping=aes(group=1)) +  
  stat_summary(fun=mean,geom="point")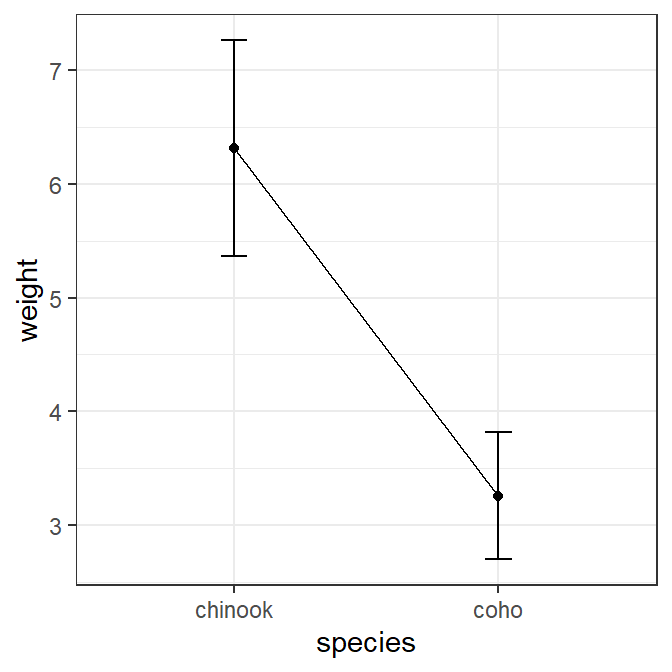

Using Marginal Means from `emmeans`

The estimated marginal means may be plotted similarly to the manually summarized means. However, the aov1mcs$emmeans data frame created above is used, which also requires using lower.CL and upper.CL for the ymin= and ymax= in geom_errorbar() and emmean for the y= mean value in geom_line() and geom_point().⁵

⁵ Review the output from aov1mcs$emmeans above taking special note of the variable names.

ggplot(data=aov1mcs$emmeans,mapping=aes(x=species)) +
  geom_errorbar(mapping=aes(ymin=lower.CL,ymax=upper.CL),width=0.1) +
  geom_line(mapping=aes(y=emmean,group=1)) +
  geom_point(mapping=aes(y=emmean))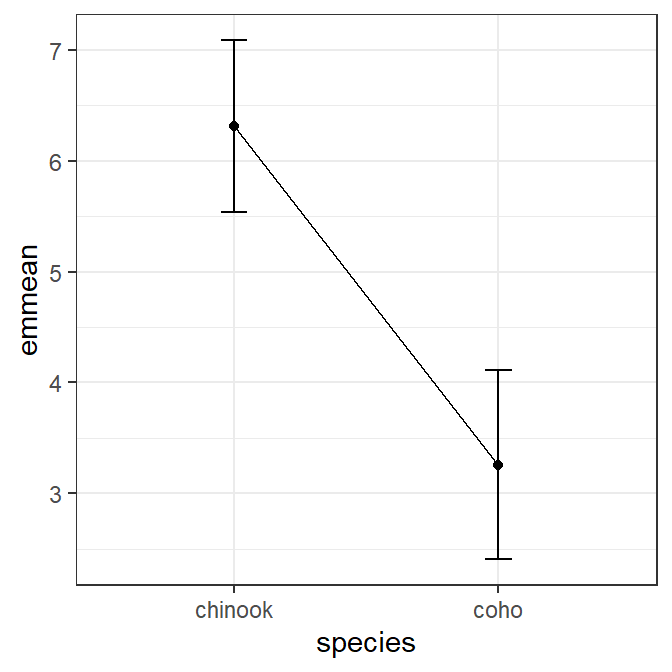

Two-Way ANOVA

The code below fits a two-way ANOVA model to examine if mean weight differs by species, by year, or by the interaction between species and year.

aov2 <- lm(weight~year*species,data=Mirex)
anova(aov2)

#R|  Analysis of Variance Table
#R|  
#R|  Response: weight
#R|                Df Sum Sq Mean Sq F value    Pr(>F)    
#R|  year           5 281.86  56.373  6.9954 1.039e-05 ***
#R|  species        1 221.69 221.689 27.5099 7.648e-07 ***
#R|  year:species   5 117.69  23.538  2.9208   0.01628 *  
#R|  Residuals    110 886.44   8.059                      
#R|  ---
#R|  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

fitPlot() from FSA used the mean with 95% confidence interval for all combinations of species and year.

FSAmisc::fitPlot(aov2)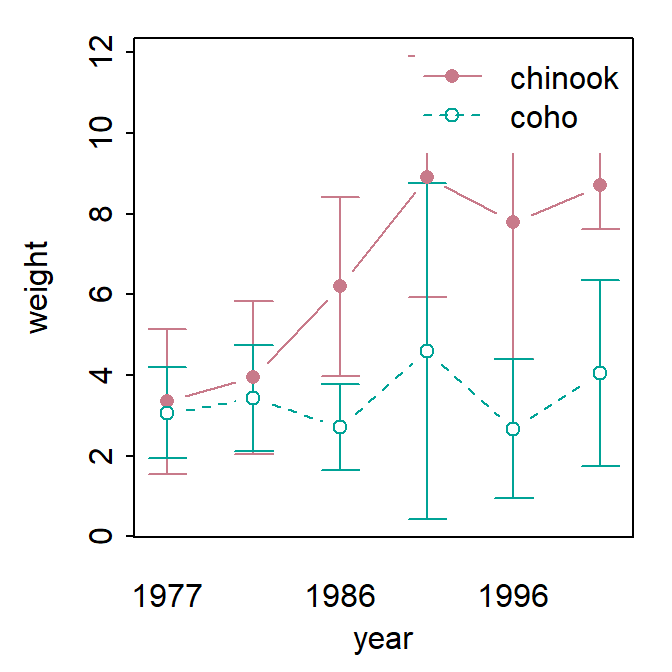

Using Built-In Functions for Summarized Means

Again, stat_summary() can be used to efficiently calculate and then plot the 95% confidence intervals and means similar to what was shown above for a one-way ANOVA. However, there are three major differences.

First, in the main ggplot() call the color of the points and lines is mapped to one of the two factor variables (species in this case) whereas the other factor variable is mapped to x=.⁶ Second, the group= aesthetic for the line geom must be set to the factor that describes how the lines should be connected, which will be the same as the variable mapped to the color aesthetic (e.g., species in this case). Third, the intervals and (possibly) the points at each level on the x-axis will overlap if they are not “dodged” a small amount.⁷ The “dodge” amount should be set outside the geom()s so that each geom uses the same amount of “dodging.” This will assure that the intervals, points, and connecting lines for each level defined by the colors align. Below this “dodge” amount is set with position_dodge() and saved to an object called pd which is then set equal to position= in each geom().

⁶ These two variables can, of course, be exchanged. However, I generally prefer to have the variable with more levels on the x-axis.

⁷ Note this same problem occurs for the fitPlot(), though there is no simple solution for it.

pd <- position_dodge(width=0.2)
ggplot(data=Mirex,mapping=aes(x=year,y=weight,color=species)) +  
  stat_summary(fun.data=mean_cl_normal,geom="errorbar",width=0.2,position=pd) + 
  stat_summary(fun=mean,geom="line",mapping=aes(group=species),position=pd) +  
  stat_summary(fun=mean,geom="point",position=pd)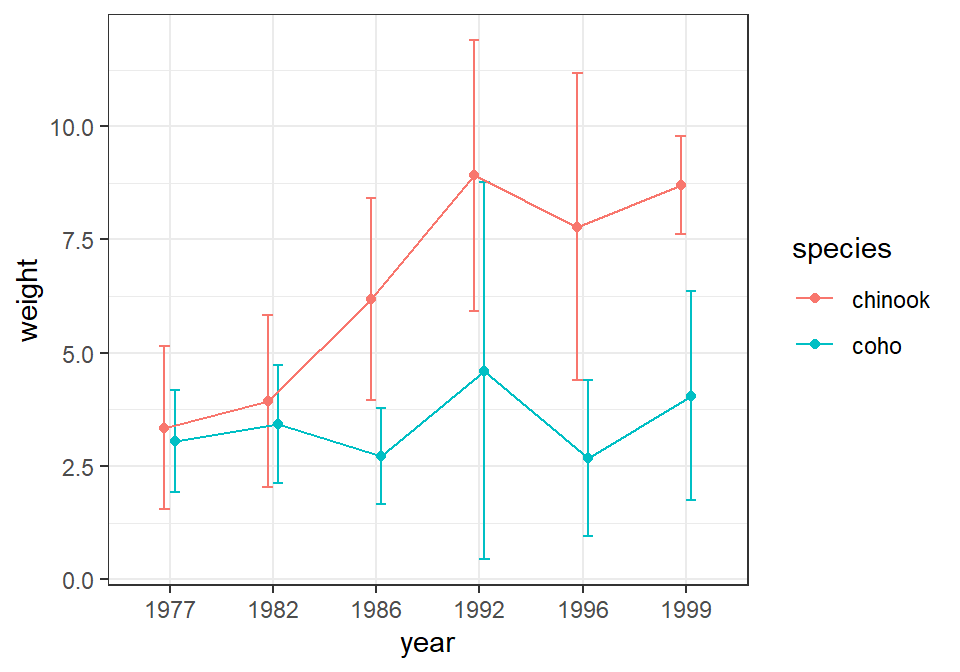

Using Marginal Means from `emmeans`

The mearginal means are again computed with emmeans(), but with year:species so that the marginal means and confidence intervals are estimated for each combination of year and species.

aov2mc <- emmeans::emmeans(aov2,specs=pairwise~year:species)
aov2mcs <- summary(aov2mc)
aov2mcs$emmeans

#R|   year species emmean    SE  df lower.CL upper.CL
#R|   1977 chinook   3.35 0.819 110    1.723     4.97
#R|   1982 chinook   3.94 0.819 110    2.319     5.57
#R|   1986 chinook   6.20 0.819 110    4.571     7.82
#R|   1992 chinook   8.91 1.073 110    6.788    11.04
#R|   1996 chinook   7.79 0.856 110    6.090     9.48
#R|   1999 chinook   8.71 0.787 110    7.148    10.27
#R|   1977 coho      3.06 0.819 110    1.436     4.68
#R|   1982 coho      3.43 0.819 110    1.808     5.06
#R|   1986 coho      2.71 0.819 110    1.090     4.34
#R|   1992 coho      4.60 1.270 110    2.084     7.12
#R|   1996 coho      2.67 1.004 110    0.681     4.66
#R|   1999 coho      4.05 1.159 110    1.753     6.35
#R|  
#R|  Confidence level used: 0.95

The plot of these marginal means is constructed similarly to that for the one-way ANOVA but using the dodging and color aesthetics described above.

pd <- position_dodge(width=0.2)
ggplot(data=aov2mcs$emmeans,mapping=aes(x=year,color=species)) +
  geom_errorbar(mapping=aes(ymin=lower.CL,ymax=upper.CL),width=0.2,position=pd) +
  geom_line(mapping=aes(y=emmean,group=species),position=pd) +
  geom_point(mapping=aes(y=emmean),position=pd)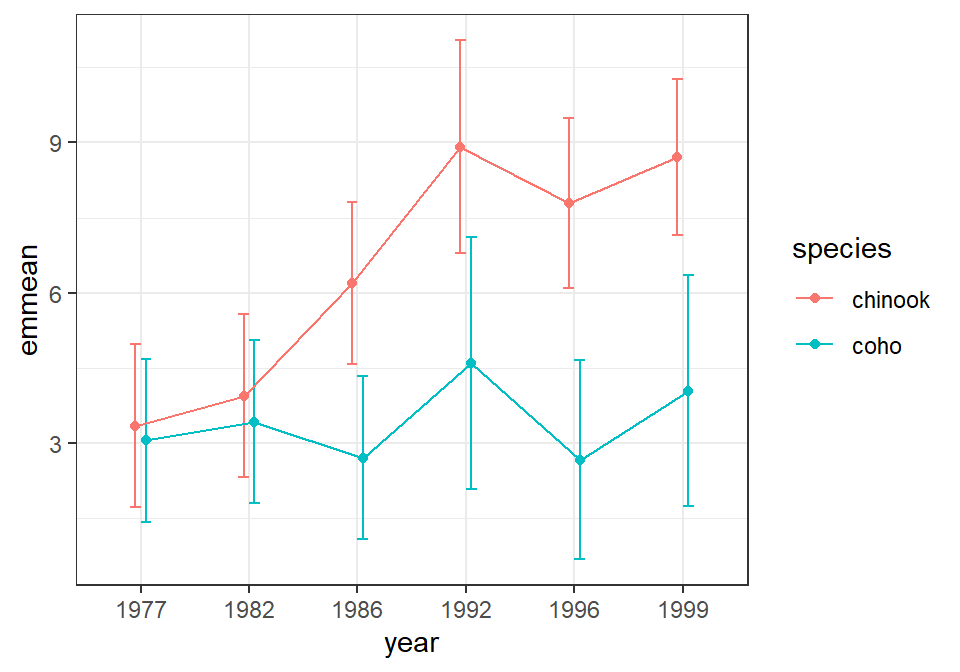

Simple Linear Regression

The code below fits a simple linear regression for examining the relationship between mirex concentration and salmon weight.

slr <- lm(mirex~weight,data=Mirex)
anova(slr)

#R|  Analysis of Variance Table
#R|  
#R|  Response: mirex
#R|             Df  Sum Sq  Mean Sq F value    Pr(>F)    
#R|  weight      1 0.22298 0.222980  26.556 1.019e-06 ***
#R|  Residuals 120 1.00758 0.008396                      
#R|  ---
#R|  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

fitPlot() from FSA showed the best-fit line with a 95% confidence band.

FSAmisc::fitPlot(slr,interval="confidence")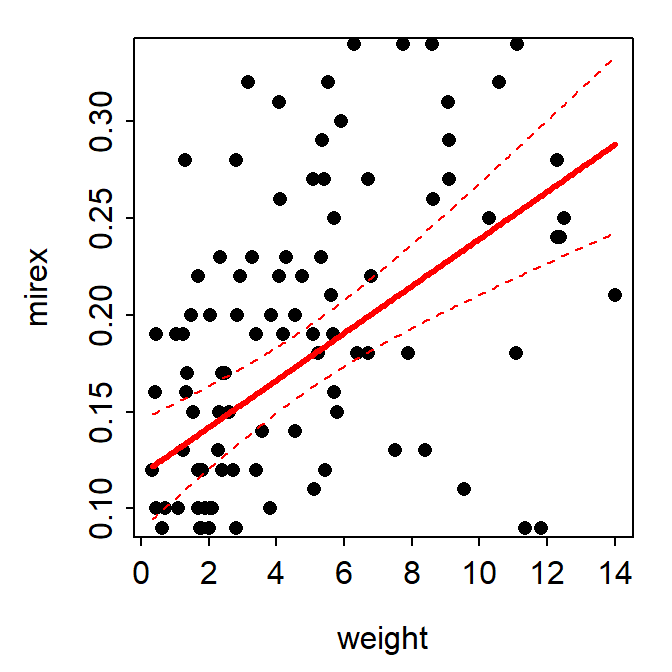

Using Manually Predicted Values I

One method for recreating this plot is to create a new data frame that first has the two variables of observed data and then adds on predicted values of the response at each observed value of the explanatory variable with 95% confidence intervals. The two observed variables are selected from the original data frame with select(). If this new data frame is given to newdata= in predict() with interval="confidence" then the predicted values (and 95% confidence intervals) will be constructed at each value of the explanatory variable. The two data frames are then column-bound together with cbind() to make one data frame for plotting (further below).

slrdf <- Mirex |>
  select(weight,mirex)
slrdf <- cbind(slrdf,predict(slr,newdata=slrdf,interval="confidence"))
peek(slrdf,n=6)

#R|      weight mirex       fit        lwr       upr
#R|  1     0.41  0.16 0.1226593 0.09588108 0.1494376
#R|  24    7.75  0.34 0.2119229 0.19088398 0.2329618
#R|  49    0.34  0.02 0.1218080 0.09477073 0.1488453
#R|  73    1.90  0.10 0.1407796 0.11907549 0.1624837
#R|  98    9.10  0.29 0.2283406 0.20287925 0.2538019
#R|  122  11.82  0.09 0.2614192 0.22530410 0.2975342

The confidence band is first plotted as a “ribbon” with the best-fit line then added followed by the observed points. In this plot, weight is globally mapped to x= in ggplot() so that it will be used for each geom. The lower and upper confidence values are mapped to ymin= and ymax= in geom_ribbon(), whereas the predicted or “fit”ted values are mapped to y= geom_line() to make the line and the observed mirex concentrations are mapped to y= in geom_point() to plot the observed points. Further note the use of alpha= to make the confidence band semi-transparent and size= to make the fitted line slightly larger than the default. Again all aspects of this plot can be changed in the usual ggplot way.

ggplot(data=slrdf,mapping=aes(x=weight)) +
  geom_ribbon(mapping=aes(ymin=lwr,ymax=upr),alpha=0.2) +
  geom_line(mapping=aes(y=fit),size=1) +
  geom_point(mapping=aes(y=mirex))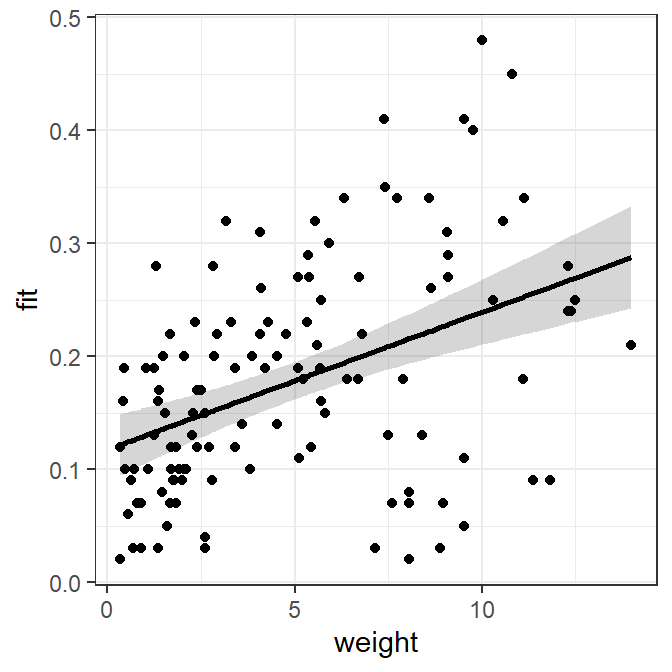

Using Manually Predicted Values II

With more sparse data sets there may not be enough predicted values to make a smooth plot. In these cases, a separate data frame with more designated values for the explanatory variable is useful. The first line below creates a data frame of weights that consists of 101 evenly spaced values from the minimum to maximum observed weight in the original data frame. Concentrations of mirex at each of these weights are then predicted from the regression line and bound to the data frame.

nd <- data.frame(weight=seq(min(slrdf$weight),max(slrdf$weight),length.out=101))
nd <- cbind(nd,predict(slr,newdata=nd,interval="confidence"))
peek(slrdf,n=6)

#R|      weight mirex       fit        lwr       upr
#R|  1     0.41  0.16 0.1226593 0.09588108 0.1494376
#R|  24    7.75  0.34 0.2119229 0.19088398 0.2329618
#R|  49    0.34  0.02 0.1218080 0.09477073 0.1488453
#R|  73    1.90  0.10 0.1407796 0.11907549 0.1624837
#R|  98    9.10  0.29 0.2283406 0.20287925 0.2538019
#R|  122  11.82  0.09 0.2614192 0.22530410 0.2975342

The plot is now constructed from two data frames – slrdf with the original observed data and nd with predicted concentrations of mirex at specifically chosen weights. Given this, the data to use must be specifically declared within each geom, with geom_ribbon() and geom_line() using the predicted data frame (i.e., nd) and geom_point() using the observed data (i.e., slrdf).

ggplot() +
  geom_ribbon(data=nd,mapping=aes(x=weight,ymin=lwr,ymax=upr),alpha=0.2) +
  geom_line(data=nd,mapping=aes(x=weight,y=fit),size=1) +
  geom_point(data=slrdf,mapping=aes(x=weight,y=mirex))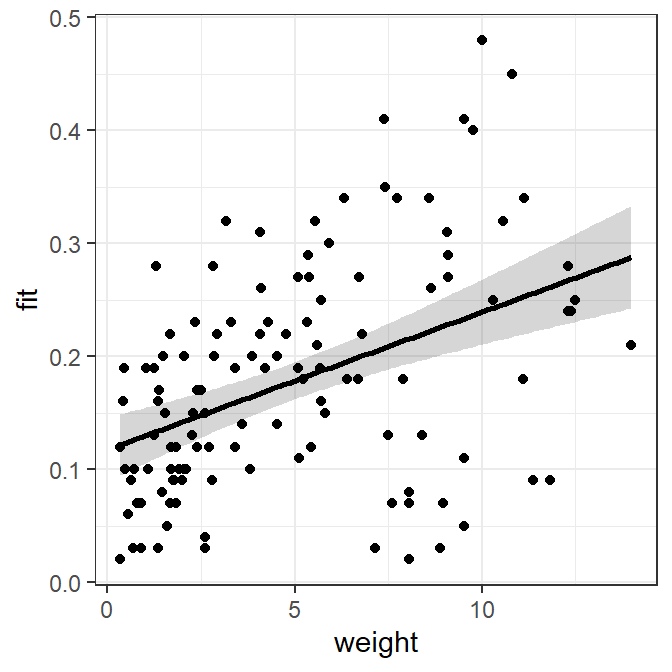

Using A Built-In Function

The best-fit line can also be added to a scatterplot with geom_smooth(), where method="lm" makes sure that a linear model is used for the “smoother.”

ggplot(data=Mirex,mapping=aes(x=weight,y=mirex)) +
  geom_smooth(method="lm",alpha=0.2) +
  geom_point()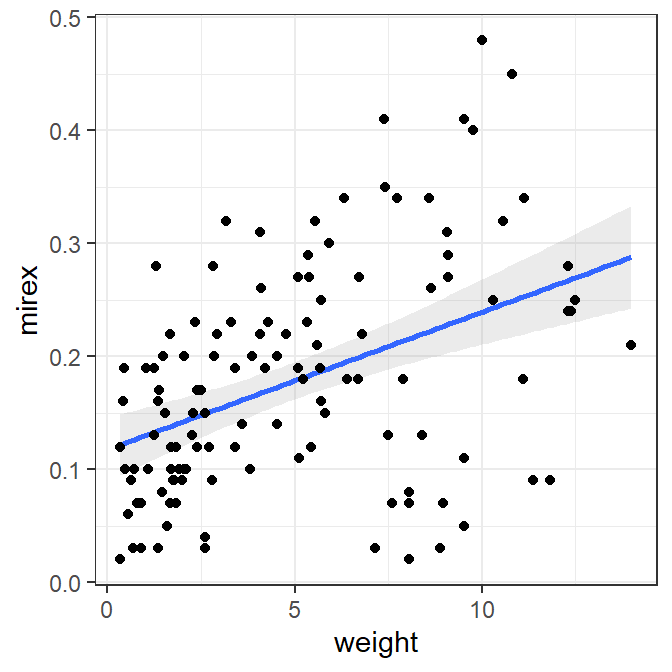

Indicator Variable Regression

The code below fits an indicator variable regression to examine if the relationship between mirex concentration and salmon weight differs betwen species.

ivr <- lm(mirex~weight*species,data=Mirex)
anova(ivr)

#R|  Analysis of Variance Table
#R|  
#R|  Response: mirex
#R|                  Df  Sum Sq  Mean Sq F value    Pr(>F)    
#R|  weight           1 0.22298 0.222980 26.8586 9.155e-07 ***
#R|  species          1 0.00050 0.000498  0.0600   0.80690    
#R|  weight:species   1 0.02744 0.027444  3.3057   0.07158 .  
#R|  Residuals      118 0.97964 0.008302                      
#R|  ---
#R|  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

fitPlot() from FSA showed the best-fit line for both species.

FSAmisc::fitPlot(ivr,interval="confidence")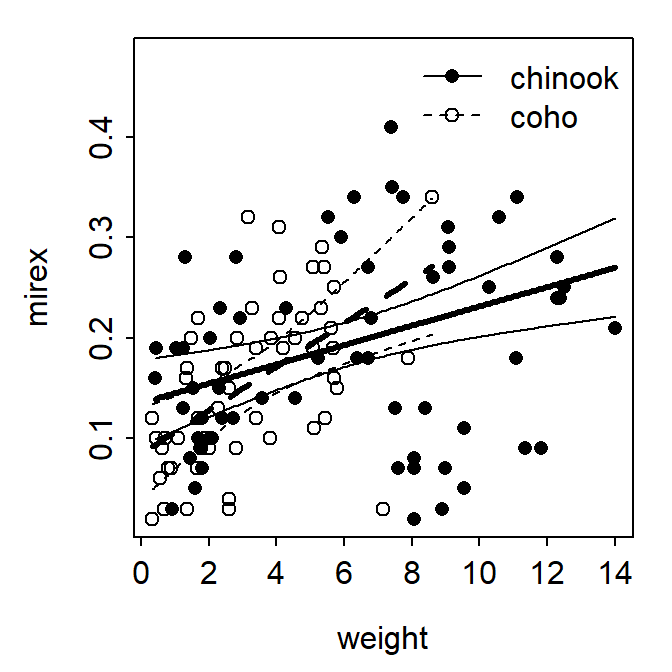

Using Manually Predicted Values

The process of constructing a similar plot in ggplot() follows the same general procedure as that for a simple linear regression. First, make a data frame that has the observed variables used in the model and predicted values and confidence limits for each observation.⁸

⁸ Again, one may want to make a data frame with more values of the explanatory variable if the observed data is sparse.

ivrdf <- select(Mirex,weight,mirex,species)
ivrdf <- cbind(ivrdf,predict(ivr,newdata=ivrdf,interval="confidence"))
peek(ivrdf,n=6)

#R|      weight mirex species        fit        lwr       upr
#R|  1     0.41  0.16 chinook 0.13939054 0.09905499 0.1797261
#R|  24    7.75  0.34 chinook 0.20990801 0.18638517 0.2334308
#R|  49    0.34  0.02    coho 0.09192064 0.04956596 0.1342753
#R|  73    1.90  0.10    coho 0.12580003 0.09660968 0.1549904
#R|  98    9.10  0.29 chinook 0.22287784 0.19567885 0.2500768
#R|  122  11.82  0.09 chinook 0.24900965 0.21056798 0.2874513

Then plot the data as before but making sure to map color= and fill= (just for the ribbon) to the species factor variable.

ggplot(data=ivrdf,mapping=aes(x=weight,color=species)) +
  geom_ribbon(mapping=aes(ymin=lwr,ymax=upr,fill=species),alpha=0.2) +
  geom_line(mapping=aes(y=fit),size=1) +
  geom_point(mapping=aes(y=mirex))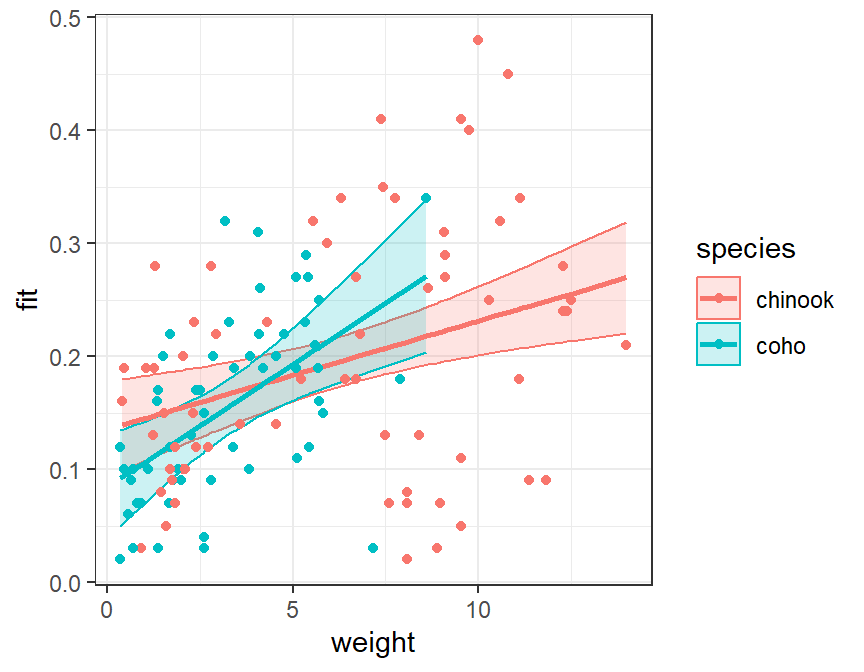

Using a Built-In Function

This plot can also be constructed with geom_smooth(), again making sure to map the color= and fill= to the species factor variable.

ggplot(data=Mirex,mapping=aes(x=weight,y=mirex,color=species,fill=species)) +
  geom_smooth(method="lm",alpha=0.2) +
  geom_point()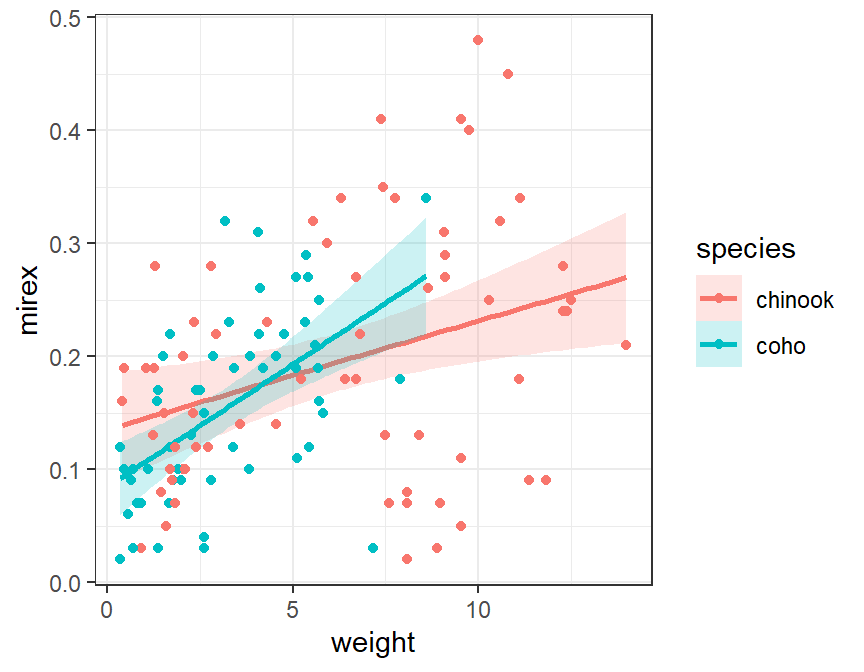

Logistic Regression

The code below fits a logistic regression to examine the relationship between the probability that mirex concentration is greater than 0.2 and salmon weight.

logreg <- glm(gt2~weight,data=Mirex,family="binomial")
summary(logreg)

#R|  
#R|  Call:
#R|  glm(formula = gt2 ~ weight, family = "binomial", data = Mirex)
#R|  
#R|  Deviance Residuals: 
#R|      Min       1Q   Median       3Q      Max  
#R|  -1.7696  -0.7462  -0.5566   0.9537   1.9789  
#R|  
#R|  Coefficients:
#R|              Estimate Std. Error z value Pr(>|z|)    
#R|  (Intercept) -2.19359    0.41871  -5.239 1.61e-07 ***
#R|  weight       0.29822    0.06496   4.591 4.41e-06 ***
#R|  ---
#R|  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#R|  
#R|  (Dispersion parameter for binomial family taken to be 1)
#R|  
#R|      Null deviance: 158.35  on 121  degrees of freedom
#R|  Residual deviance: 132.32  on 120  degrees of freedom
#R|  AIC: 136.32
#R|  
#R|  Number of Fisher Scoring iterations: 3

fitPlot() from FSA showed the fitted logistic regression curve with the observed values transparently at the top and bottom of the y-axis and symbols at the proportion of “successes” for “windows” of the x-axis.

FSAmisc::fitPlot(logreg)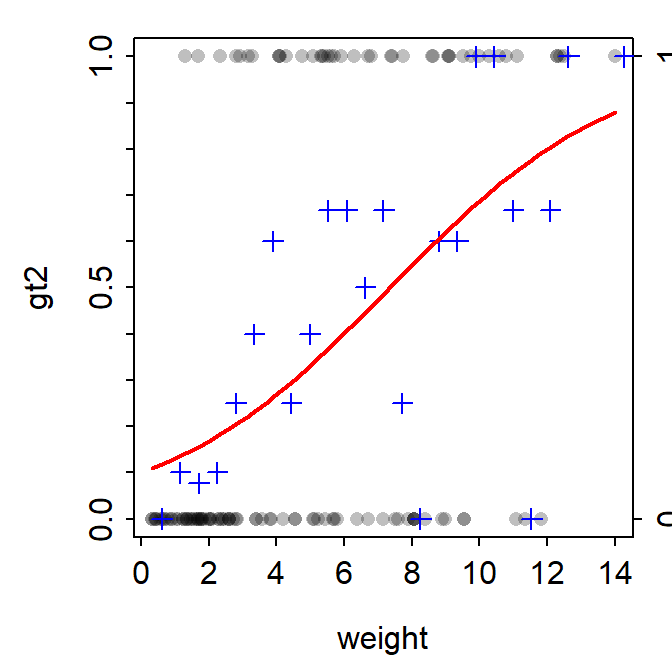

Using Manually Predicted Values

The first method for showing the logistic regression curve follows the general methodology for simple linear regression shown above. Note, however, that predict() does not produce confidence interval values for a logistic regression. Thus, the plot created in this way cannot have a confidence band.

logregdf <- select(Mirex,gt2,weight)
logregdf$fit <- predict(logreg,newdata=logregdf,
                        type="response",interval="confidence")
peek(logregdf,n=6)

#R|      gt2 weight       fit
#R|  1     0   0.41 0.1119161
#R|  24    1   7.75 0.5293765
#R|  49    0   0.34 0.1098580
#R|  73    0   1.90 0.1642466
#R|  98    1   9.10 0.6272046
#R|  122   0  11.82 0.7910738

ggplot(data=logregdf,mapping=aes(x=weight)) +
  geom_point(mapping=aes(y=gt2),alpha=0.25) +
  geom_line(mapping=aes(y=fit),size=1)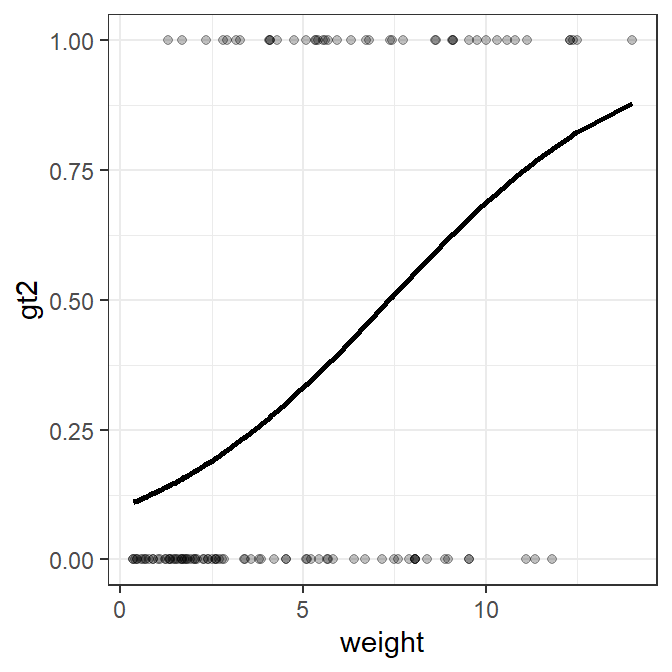

Using a Built-In Function

The best-fit logistic regression curve with a confidence band can, however, be added to a scatterplot with geom_smooth(). In this case, method= must be changed to glm and method.args= must be used as shown below so that glm will construct a logistic (rather than linear) regression.

ggplot(data=Mirex,mapping=aes(x=weight,y=gt2)) +
  geom_smooth(method="glm",alpha=0.2,method.args=list(family="binomial")) +
  geom_point(alpha=0.25)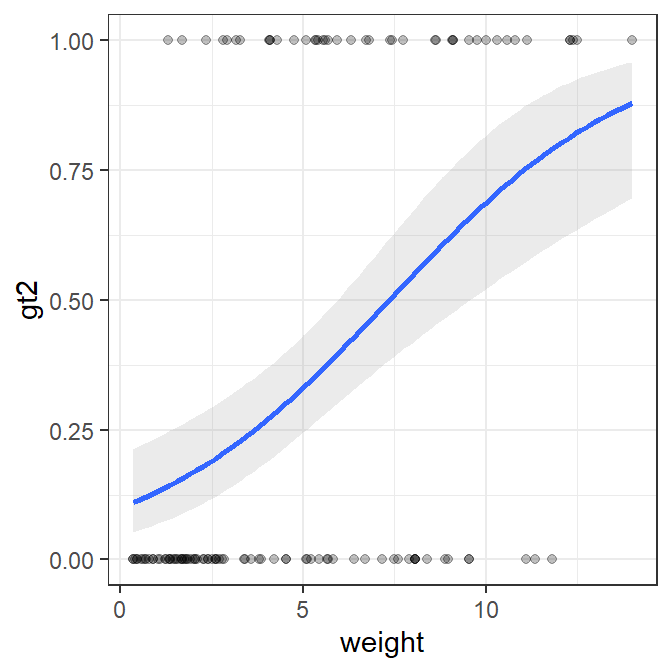

Note that this method easily generalizes to an indicator variable logistic regression (note that color= and fill= are mapped to the species factor variable).

logreg2 <- glm(gt2~weight*species,data=Mirex,family="binomial")

ggplot(data=Mirex,mapping=aes(x=weight,y=gt2,color=species,fill=species)) +
  geom_smooth(method="glm",alpha=0.2,
              method.args=list(family="binomial")) +
  geom_point(alpha=0.25)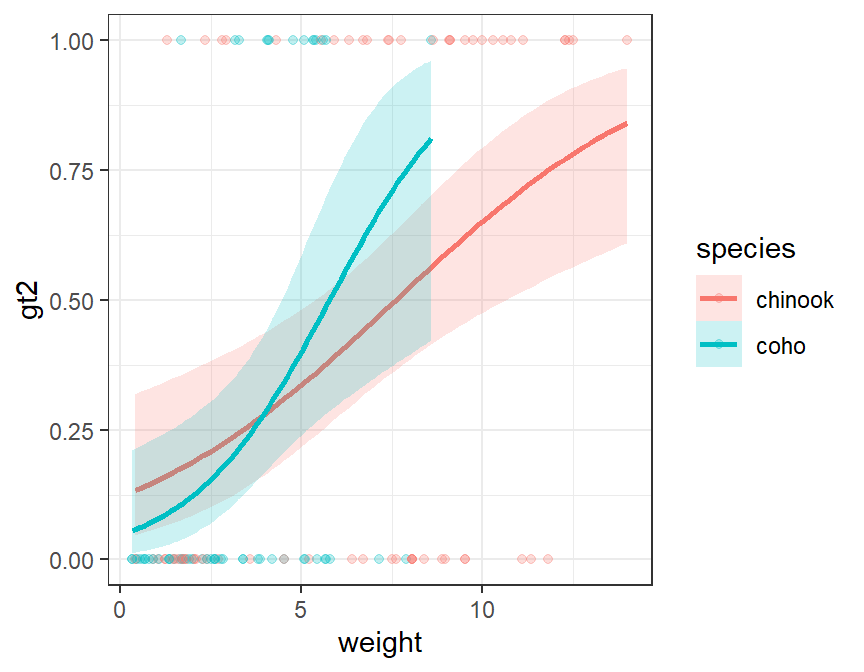

Polynomial Regression

The code below fits a quadratic (second degree polynomial) regression for the relationship between mirex concentration and salmon weight.

poly2 <- lm(mirex~weight+I(weight^2),data=Mirex)
summary(poly2)

#R|  
#R|  Call:
#R|  lm(formula = mirex ~ weight + I(weight^2), data = Mirex)
#R|  
#R|  Residuals:
#R|        Min        1Q    Median        3Q       Max 
#R|  -0.208068 -0.048257  0.000994  0.060883  0.244424 
#R|  
#R|  Coefficients:
#R|                Estimate Std. Error t value Pr(>|t|)    
#R|  (Intercept)  0.0875361  0.0209754   4.173 5.74e-05 ***
#R|  weight       0.0283282  0.0086331   3.281  0.00136 ** 
#R|  I(weight^2) -0.0013524  0.0006953  -1.945  0.05413 .  
#R|  ---
#R|  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#R|  
#R|  Residual standard error: 0.09059 on 119 degrees of freedom
#R|  Multiple R-squared:  0.2064,   Adjusted R-squared:  0.1931 
#R|  F-statistic: 15.48 on 2 and 119 DF,  p-value: 1.06e-06

fitPlot() from FSA showed the best-fit regression curve.

FSAmisc::fitPlot(poly2,interval="confidence")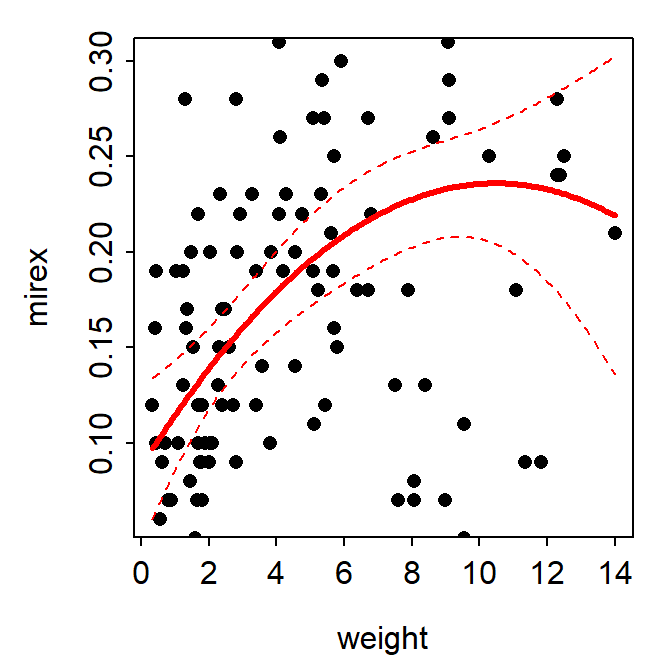

Using Manually Predicted Values

This regression can be viewed similarly to the way the simple linear regressions was viewed.

polydf <- select(Mirex,weight,mirex)
polydf <- cbind(polydf,predict(poly2,newdata=polydf,interval="confidence"))
ggplot(polydf,mapping=aes(x=weight)) +
  geom_ribbon(mapping=aes(ymin=lwr,ymax=upr),alpha=0.2) +
  geom_line(mapping=aes(y=fit),size=1) +
  geom_point(mapping=aes(y=mirex))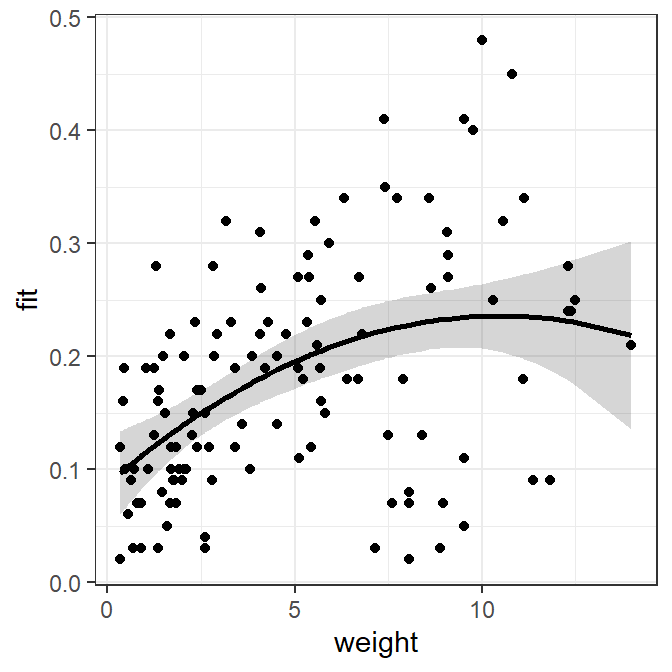

Using a Built-In Function

This type of regression can also be viewed using geom_smooth() but the formula for the polynomial must be given to formula=. However, note that in this formula you put y and x rather than the names of the variables that are mapped to y and x.

ggplot(data=Mirex,mapping=aes(x=weight,y=mirex)) +
  geom_smooth(method="lm",formula="y~x+I(x^2)",alpha=0.2) +
  geom_point()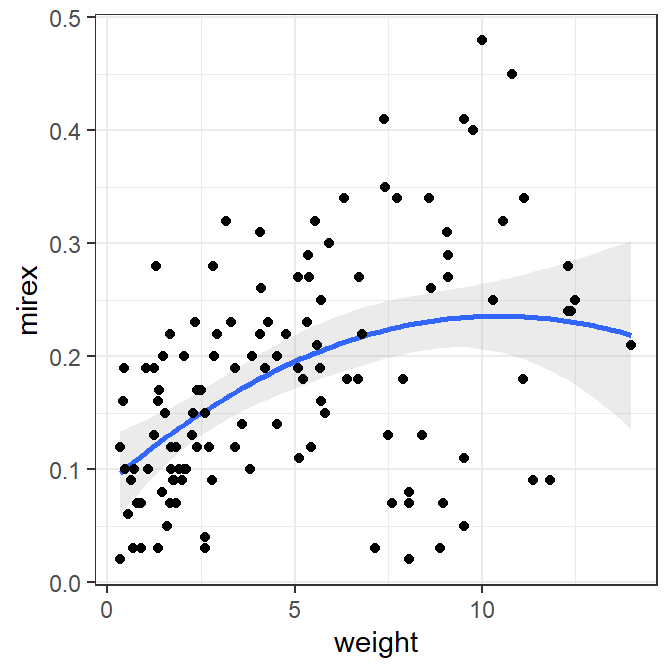

Nonlinear Regression

The concepts about producing a fitted line plot for a non-linear regression in ggplot is described in detail, with respect to a von Bertalanffy growth function, in this post and this post.

Conclusion

fitPlot() in FSA was removed in early 2022. This post describes a more transparent (i.e., not a “black box”) and flexible set of methods for constructing similar plots using ggplot2 for those who will need to transition away from using fitPlot().

As mentioned in the examples above, each plot can be modified further using typical methods for ggplot2. These changes were not illustrated above to minimize the amount of code shown in this post. However, as an example, the code below shows a possible modification of the IVR plot shown above.

ggplot(data=Mirex,mapping=aes(x=weight,y=mirex,color=species,fill=species)) +
  geom_smooth(method="lm",alpha=0.1,size=1.25) +
  geom_point(size=1.5) +
  scale_y_continuous(name="Mirex Concentration in Tissue",limits=c(0,0.5),
                     expand=expansion(mult=0)) +
  scale_x_continuous(name="Salmon Weight (kg)",limits=c(0,15),
                     expand=expansion(mult=0)) +
  scale_color_manual(values=c("#E69F00","#0072B2"),
                     aesthetics=c("color","fill")) +
  theme(panel.grid.major=element_line(color="gray90",linetype="dashed"),
        panel.grid.minor=element_blank(),
        axis.title=element_text(size=rel(1.25)),
        axis.text=element_text(size=rel(1.1)),
        legend.position=c(0,1),
        legend.justification=c(-0.05,1.02),
        legend.title=element_blank(),
        legend.text=element_text(size=rel(1.1)))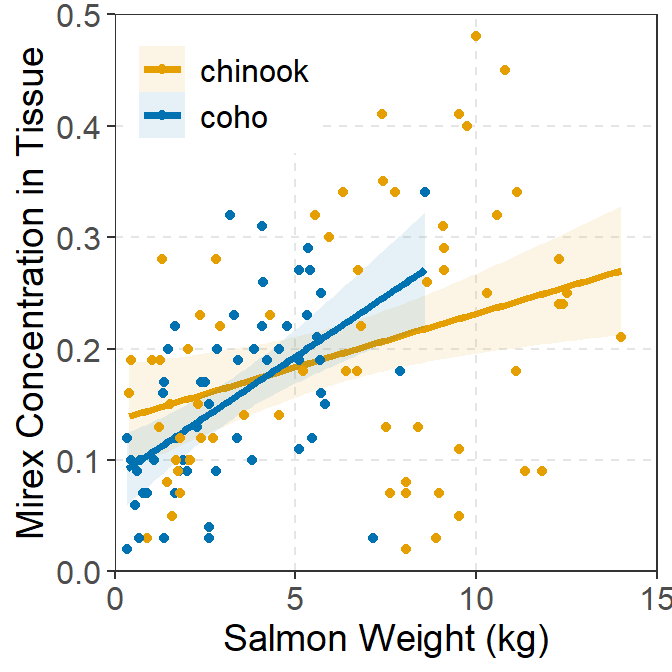

Reuse

https://creativecommons.org/licenses/by/4.0/

Citation

BibTeX citation:

@online{h. ogle2021,
  author = {H. Ogle, Derek},
  title = {Replace {fitPlot()} with Ggplot},
  date = {2021-05-25},
  url = {https://fishr-core-team.github.io/fishR//blog/posts/2021-5-25_fitPlot-replacement},
  langid = {en}
}

For attribution, please cite this work as:

H. Ogle, D. 2021, May 25. Replace fitPlot() with ggplot. https://fishr-core-team.github.io/fishR//blog/posts/2021-5-25_fitPlot-replacement.

Introduction

Example Data

One-Way ANOVA

Using Manually Summarized Means

Using Built-In Functions for Summarized Means

Using Marginal Means from emmeans

Two-Way ANOVA

Using Built-In Functions for Summarized Means

Using Marginal Means from emmeans

Simple Linear Regression

Using Manually Predicted Values I

Using Manually Predicted Values II

Using A Built-In Function

Indicator Variable Regression

Using Manually Predicted Values

Using a Built-In Function

Logistic Regression

Using Manually Predicted Values

Using a Built-In Function

Polynomial Regression

Using Manually Predicted Values

Using a Built-In Function

Nonlinear Regression

Conclusion

Reuse

Citation

Using Marginal Means from `emmeans`

Using Marginal Means from `emmeans`