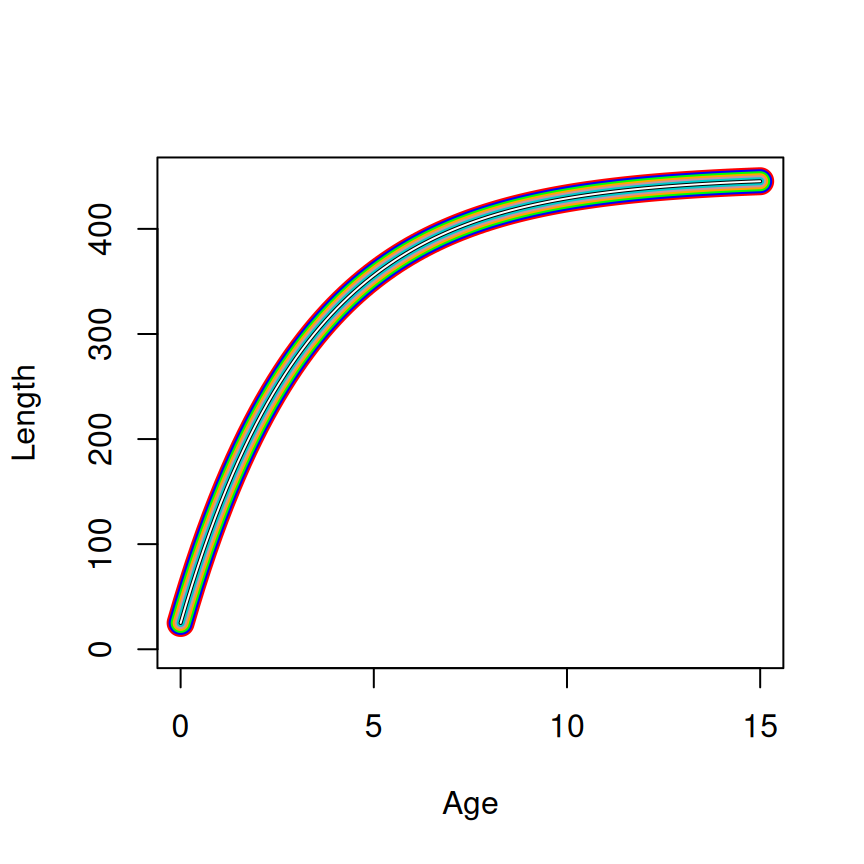
SSasymp (=450, =25, and =-1.2). The linewidth decreases from the first to last parameterization (and the color differs) to show how the curves are plotted on top of each other.

2026-01-09
Source:vignettes/articles/Growth_Starting_Values.qmd
The most common growth models used in fisheries, such as von Bertalanffy, Gompertz, logistic, and Richards, are non-linear models. Computer functions used to estimate parameters for these models require “starting values” to initiate the parameter search algorithm. Previous versions of FSA (v0.9.6 and lower) used ad hoc methods to estimate starting values for parameterizations of the von Bertalanffy function, but did not provide any method to derive starting values for the ohter common growth functions.
Several “self-starting” non-linear models are provided in R, with three of these found in base R and one in an add-on package that correspond to the common fisheries growth models. These functions provide starting values that are based on robust theory. Herein, I show how the starting values provided by these self-starting functions can be used to derive starting values for the common parameterizations of the common growth models used in fisheries. I will conclude by briefly demonstrating a new function in FSA that will provide the starting values demonstrated here.
FSA provides a wide variety of von Bertalanffy parameterizations for modeling simple length-at-age data (Table 1).1
FSA.
| param | Equation |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | where |
The response variable, , is length and the explanatory variable, is age. Parameters in these growth functions are:
Constant values (i.e., set by the user) are:
SSasymp() is a self-starting function2 to fit an “asymptotic regression” function to data. The parameterization for this function is3
where and are the response and explanatory variables, respectively, is a parameter for the horizontal (i.e., ) asymptote, is a parameter related to the value of at , and is a “parameter representing the natural logarithm of the rate constant.”
In growth (in length) modeling, is (for length); is (for time as measured by age); is clearly , the asympotic mean length; and is clearly , the mean length at (i.e., the y-intercept). Thus, at this point, the R “asymptotic regression” function can be re-written for the purposes of growth modeling as
If we move off of the log scale by defining , we can further write this function as
Equation 1 is exactly the second parameterization of the von Bertalanffy growth function in FSA.4 Thus, the starting values produced by SSasymp() can be used directly to find starting values for the second parameterization of the von Bertalanffy growth function in FSA (Table 2). Indeed these values can be used for all parameterizations that have , , and . Starting values for other parameters in other parameterizations are derived from these values as shown below.
A starting value for , the “hypothetical time when the mean length is zero”, is derived by setting in Equation 1 and solving for .
The parameter was introduced into the fisheries growth modeling literature as (Gallucci and Quin 19795). Thus, a starting value for is simply the product of the starting values for and .
A starting value for is derived (most easily) by solving the first parameterization equation for when .
A starting value for (i.e., mean length at time ) can be found by simply plugging into any parameterization6 and solving for . This strategy generalizes to find starting values for , , and .
A starting value for can be found by plugging for into any of the parameterizations and solving for .
SSasymp() parameters (, , and ) to parameters for the common von Bertalanffy parameterizations used to model fish growth in FSA. Note that parameterizations 6, 7, and 8 have other parameters not shown in this table (but described in the main text).
| Param | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 |
The equivalency of the parameterizations and the starting values across parameterizations is shown in Figure 1.

SSasymp (=450, =25, and =-1.2). The linewidth decreases from the first to last parameterization (and the color differs) to show how the curves are plotted on top of each other.
The ninth parameterization (Table 3) of the von Bertalanffy model in FSA is a so-called “double von Bertalanffy” model.7
FSA.
| param | Equation |
|---|---|
| 9 |
Starting values for the ninth parameterization (i.e., the “double”) von Bertalanffy growth model have not been developed in FSA. Starting values for this parameterization will have to be developed by other means.
There are also several parameterizations of the von Bertalanffy model that include a seasonal component in the model for when age is not recorded annually (Table 4).
FSA.
| param | Equation |
|---|---|
| 10 | where |
| 11 | where |
| 12 | where |
New parameters in these growth functions are:8
Starting values for , , and are derived as if the data were recorded as annual lengths-at-age. Starting values for the other parameters are defined ad hoc as follows.
Starting values for the seasonal growth models are much less tested than those for annual growth models. Please consider them carefully.
Still other parameterizations of the von Bertalanffy model are used with tag-recapture data (Table 5).
FSA.
| param | Equation |
|---|---|
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | with and |
The response variable is generally the change in length (i.e., growth increment) from time of tagging to time of recapture, . Some models are parameterized to have on the right-hand-side though. The explanatory variable is the change in time between the time of tagging and recapture, .
New parameters in these growth functions are:
Starting values for (most of) these parameters were developed with the following ad hoc procedure.
FSA at the 10th and 90th percentiles of observed for the other parameterizations.]In the Wang models is 0 if there is no individual variation in growth. In my experience a starting value for near 0, but no 0, is usually sufficient. FSA defaults to use as a starting value. A starting value for of is used by noting that if then parameterizations 15 and 16 are equal when . An average can be estimated by using for . These starting values for and have not been rigorously tested.
Warning
Starting values for parameterization 19 have not been developed for
FSA. Starting values for this parameterization will have to be developed by other means.
FSA provides several parameterizations of the Gompertz function for modeling simple length-at-age data (Table 6).
FSA.
| param | Equation |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
New parameters in these growth functions are:9
SSgompertz() is a self-starting function10 to fit a Gompertz function to data. The parameterization for this function is11
where and are the response and explanatory variables, respectively, is a parameter for the horizontal (i.e., ) asymptote, is a parameter related to the value of at , and is a “parameter related to the scale of the x-axis.”
In growth (in length) modeling, is (for length), is (for time as measured by age), and is clearly . Thus, at this point, the Gompertz function from SSgompertz() can be re-written for the purposes of growth modeling as
It is not immediately clear how and relate to parameters from common parameterizations of the Gompertz functions used to model fish growth. These will be explained below.
The first parameterization differs from Equation 2 only in the exponent of (after the negative). This part of the equation for the first parameterization can be rearranged as follows
If and then this simplified exponent is the same as the exponent in Equation 2. Thus, and (and, of course, ).
Similarly, the second parameterization also only differs from Equation 2 after the negative in the exponent of . Again, simplifying this exponent gives
If and then this simplified exponent is the same as the exponent in Equation 2. Thus, and .
There is no asymptote in the third parameterizations, so the entire function must be manipulated to show equivalence to Equation 2.
If , , and, again, then the third parameterization is equivalent to Equation 2. Thus, , , and .
The fourth parameterization is equal to Equation 2 if and . Thus, again and (and, of course, ).
The fifth parameterization includes which appears to be defined, as in the von Bertalanffy function, as the age where the mean length is zero (i.e., the x-intercept). The three-parameter Gompertz function used here has a lower asymptote at and, thus, does not have an x-intercept. Therefore, it is not exactly clear what is. However, again, the exponent of (after the negative) of the fifth parameterizations can be rearranged
If and , then this simplified exponent is the same as the exponent in Equation 2. Thus, and (and, of course, ).
These findings are summarized in Table 7.
SSgompertz() parameters (, , and ) to parameters for the common Gompertz parameterizations used to model fish growth in FSA.
| param | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 |
The equivalency of the parameterizations and the starting values across parameterizations is shown in Figure 2.
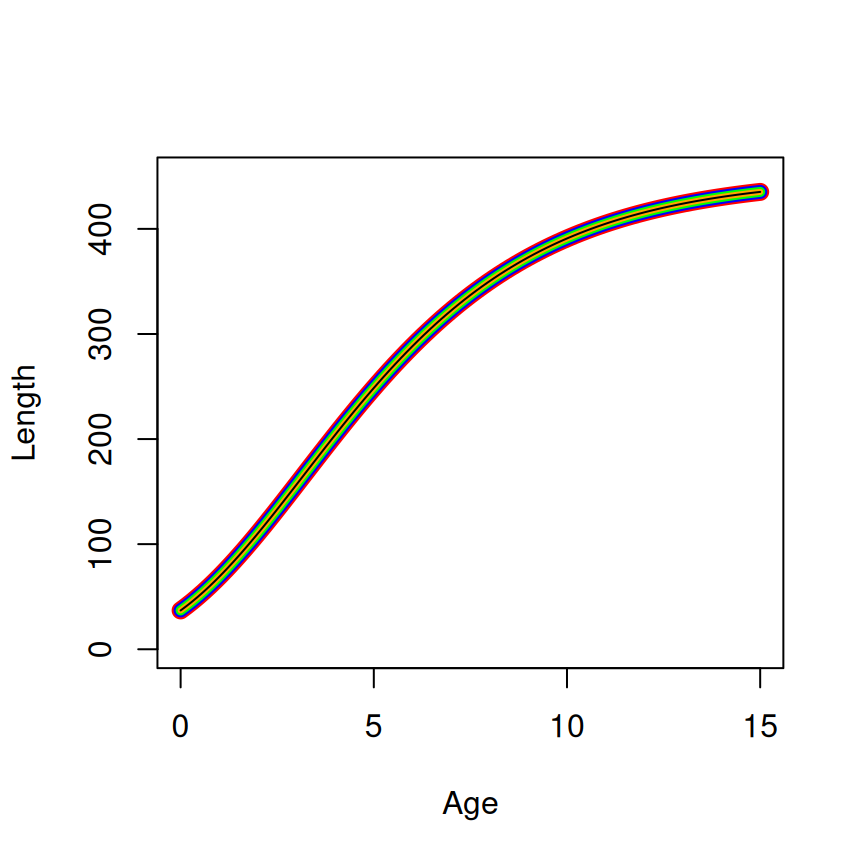
SSgompertz (=450, =2.5, and =0.75). The linewidth decreases from the first to last parameterization (and the color differs) to show how the curves are plotted on top of each other.
Still other parameterizations of the Gompertz model are used with tag-recapture data (Table 8).
FSA.
| param | Equation |
|---|---|
| 6 | |
| 7 |
Warning
Starting values for the tag-recapture growth models have not been developed for
FSA. Starting values for these parameterizations will have to be developed by other means.
FSA provides several parameterizations of the logistic function for modeling simple length-at-age data (Table 9).
FSA.
| param | Equation |
|---|---|
| 1 | |
| 2 | |
| 3 |
The response variable, , is the mean length and the explanatory variable, is age. Parameters in these growth functions are:12
SSlogis() is a self-starting function13 to fit a logistic function to data. The parameterization for this function is14
where and are the response and explanatory variables, respectively, is a parameter for the horizontal (i.e., ) asymptote, is a parameter for the value of at the inflection point, and is a “parameter on the input axis.”
In growth (in length) modeling, is (for length), is (for time as measured by age), and is clearly . Most likely is , but it is not clear at this point. Thus, at this point, the R logistic function can be re-written for the purposes of growth modeling as
Below I show how parameters in the common parameterizations of the logistic function relate to and (and, possibly, ). It is easier to relate Equation 3 to the Gompertz paramaeterizations if Equation 3 is presented in the more verbose form of
The only difference between the first parameterization and Equation 3 is in the denominator after the “1+”. This portion of the equation for the first parameterization can be rewritten as
Comparing this to Equation 4 it is apparent that and . The latter can be simplified as
Thus, is the abcissa of the inflection point. Starting values for the first parameterization are thus , , and .
The second paramaterization only differs from Equation 3 in the denominator after the “1+”, and no simplification is needed to notice that and .
The third parameterizations differs more substantively and requires more work. First, rewrite the whole equation by dividing both the numerator and denominator by to get
In this form the only difference from Equation 3 is again in the denominator after the “1+”. Again, by comparing this to Equation 4, it is apparent that and . This second value is solved for with
These findings are summarized in Table 10.
SSlogis() parameters (, , and ) to parameters for the common logistic parameterizations used to model fish growth in FSA.
| param | |||||
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 |
The equivalency of the parameterizations and the starting values across parameterizations is shown in Figure 3.
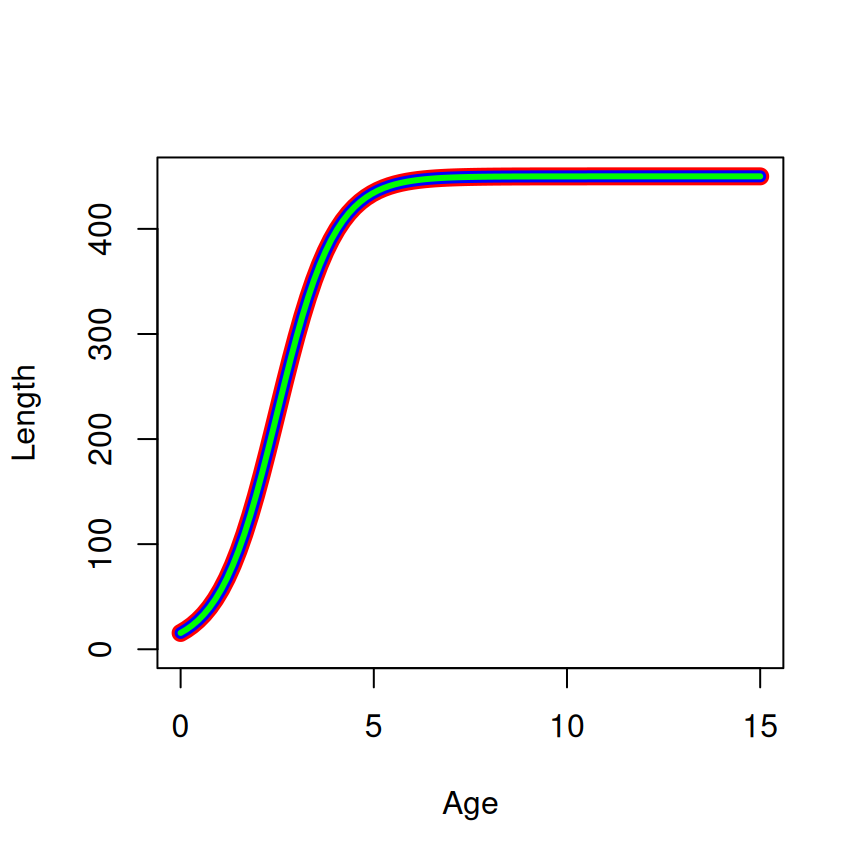
SSlogis (=450, =2.5, and =0.75). The linewidth decreases from the first to last parameterization (and the color differs) to show how the curves are plotted on top of each other.
FSA provides several parameterizations of the Richards function for modeling simple length-at-age data (Table 11).
FSA.
| param | Equation |
|---|---|
| 1 | |
| 2 | |
| 3 |
The response variable, , is the mean length and the explanatory variable, is age. New parameters in these growth functions are:15
The FlexParamCurve package contains SSposnegRichards() which is a self-starting function for using nls() to fit a “Positive-Negative Richards growth” function to data. This function can fit an 8-parameter curve but if some of the parameters are not used then it is possible to fit a 4-parameter Richards function, a function similar to the Richards parameterizations in FSA. Their “twelfth model” (i.e., modno=12) can be written, using their R function parameters, as
where and are the response and explanatory variables, respectively, is a parameter for the horizontal (i.e., ) asymptote, is a “rate parameter”, is the “inflection point” (i.e., the x-axis position of the inflection point), and is a “shape parameter”.
To better match the parameterizations in FSA, the FlexParamCurve function can be re-written as,
In growth (in length) modeling, is (for length), is (for time as measured by age). With these substitutions the (modified) function from FlexParamCurve can be re-written for the purposes of growth modeling as
A comparison of Equation 5 to the three parameterizations of the Richards function in FSA clearly shows that and for each. Substituting these values, and noting that , Equation 5 can be written as
This is exactly the first parameterization in FSA if and . In fact, and in the other parameterizations.
If is the value of when then plug 0 into Equation 5 and solve for as follows16
or, alternatively, .
In the third parameterization is defined as the mean length when . Thus, plug into Equation 5 and solve for to see that .
These findings are summarized in Table 12.
SSposnegRichards() parameters (, , , and ) to parameters for the common Richards parameterizations used to model fish growth in FSA.
| param | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 |
The equivalency of the parameterizations and the starting values across parameterizations is shown in Figure 3.

SSposnegrichards (=450, =2.5, =0.5, =0.1). The linewidth decreases from the first to last parameterization (and the color differs) to show how the curves are plotted on top of each other.
Schnute (1981) proposed a model for fish growth that can represent the von Bertalanffy, Gompertz, logistic, and Richards functions, along with others. The model has the following four parameters
Starting values for and are easily obtained as the mean observed lengths at ages and . However, I am unaware of any robust methodological method for developing starting values for and . Descriptions in Schnute (1981) suggest that is equal to from the von Bertalanffy or from the Richards, if growth is shaped like those functions. A good “wild guess” at and is 0.3, so FSA used 0.3 as an ad hoc “wild guess” starting value for . Further discussion in Schnute (1981) of the shape of growth trajectories relative to suggests that is likely not negative for most fisheries length-at-age data.
No similar observations were made with respect to from reading Schnute (1981). Limited personal experience suggests that using a starting value for are fickle. For cases 1 and 2, a “small” tends to work, so a starting value of 0.5 is used for in FSA. For case 3, a “larger” is needed, so a staring of 3.0 is used for in FSA. These starting values are “wild guess” at best and are unlikely to work in all (or even nost) situations. See the examples at the end of this article for how to manually choose starting values with FSA.
Finally, it seems that the automatic generation of stating values algorithm tends to work better if is very near, if not the actual, youngest observed age. In contrast, seems to work better if it is near the start (i.e., younger age) rather than the end of the asymptote.
In FSA versions >0.9.6, findGrowthStarts() can be used to find the starting values described here. This function has four main parameters. The first two are a formula of the form length~age and data= which contain the length and age data from which the starting values will be derived. Additionally, use type= to choose the type of growth function to be used (i.e., "von Bertalanffy", "Gompertz", "logistic", or "Richards") and param= to choose the particularly parameterization for the model by the number shown in Table 1, Table 4, Table 6, Table 9, and Table 11.
For example, suppose that length-at-age data similar to that shown below is available in a data.frame named df.
#> age tlV
#> 0 61
#> 2 237
#> 3 287
#> 4 312
#> 7 430
#> 15 435The starting values for the first parameterization of the von Bertalanffy model could be obtained as below.
( sv1 <- findGrowthStarts(tlV~age,data=GrowthData1,type="von Bertalanffy",param=1) )
#> Linf K t0
#> 454.4806075 0.2974555 -0.4752262It is also possible to declare the model parameterization with a “name.”17
( sv1 <- findGrowthStarts(tlV~age,data=GrowthData1,type="von Bertalanffy",pname="Typical") )
#> Linf K t0
#> 454.4806075 0.2974555 -0.4752262There may be times when the provided starting values are non-sensical (you may get a warning message) or they do not lead to model convergence when fitting the non-linear regression to data. In these instances it may be useful to view a quick diagnostic plot of how the model evaluated at the starting values “fits” the data. Such a plot can be made by including plot=TRUE in findGrowthStarts().
sv1 <- findGrowthStarts(tlV~age,data=GrowthData1,type="von Bertalanffy",param=1,
plot=TRUE)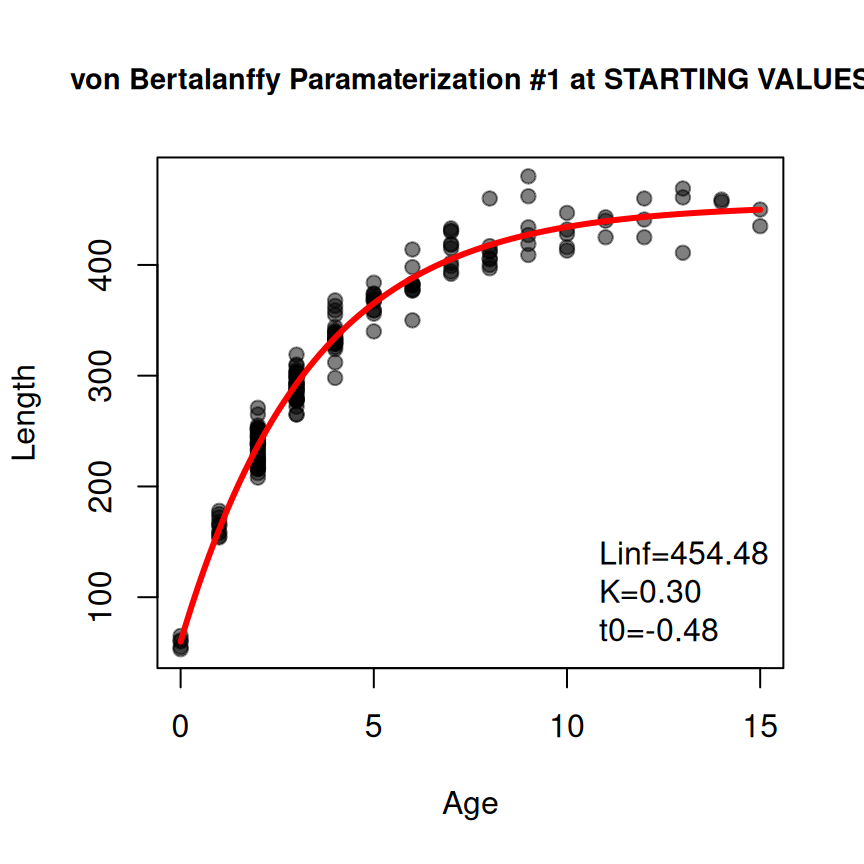
Additionally, it may be useful to “fix” some starting values at values of your choice (rather than having them determined from the data). Such parameters can be included in a NAMED vector given to fixed= in findGrowthStarts(). For example, the K parameter is fixed at 0.5 below.
( sv2 <- findGrowthStarts(tlV~age,data=GrowthData1,type="von Bertalanffy",param=1,
fixed=c("K"=0.5)) )
#> Linf K t0
#> 454.4806075 0.5000000 -0.2827173Some parameterizations of the von Bertalanffy require the user to choose values for certain constants. For example, param=7 requires you to choose a “young” age for t1 and an “older” age for t2. These constants should be set in a NAMED vector that is given to constvals= in findGrowthStarts().
( sv3 <- findGrowthStarts(tlV~age,data=GrowthData1,type="von Bertalanffy",param=7,
constvals=c("t1"=1,"t3"=13)) )
#> L1 L3 K
#> 161.4312295 446.2251430 0.2974555Of course, all of these optional arguments may be used together.18
sv4 <- findGrowthStarts(tlV~age,data=GrowthData1,type="von Bertalanffy",param=7,
constvals=c("t1"=1,"t3"=13),fixed=c("K"=0.5),plot=TRUE)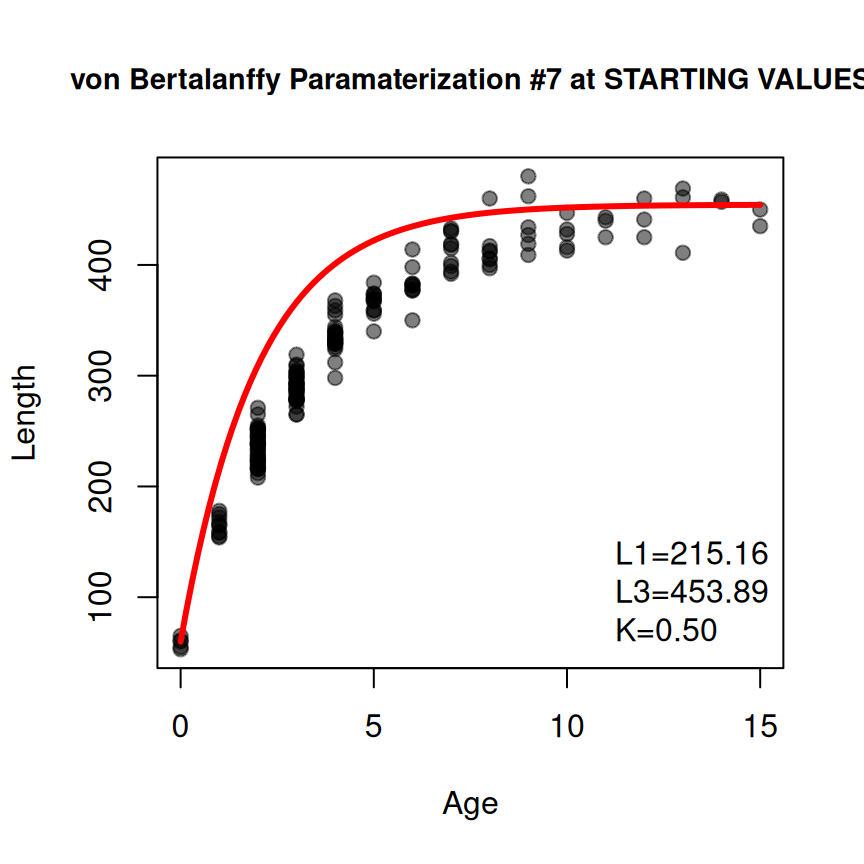
Of course, similar code is used for the other growth models (and parameterizations).
( sv5 <- findGrowthStarts(tlV~age,data=GrowthData1,type="Gompertz",param=2) )
#> Linf gi ti
#> 443.5949291 0.4521523 1.1615297It is important to note that these are examples of find the starting values only. These starting values would then be provided to a nonlinear model fitting algorithm (e.g., nls()) to find the best-fit parameter estimates. This is demonstrated more thoroughly elsewhere, but below is a quick example using the starting values for first parameterization of von Bertalanffy derived above.
vonb1 <- makeGrowthFun(type="von Bertalanffy")
rvb1 <- nls(tlV~vonb1(age,Linf,K,t0),data=GrowthData1,start=sv1)
coef(rvb1)
#> Linf K t0
#> 456.0374952 0.2932701 -0.4848237